Dynamic stochastic economic models normally build on the assumption of time-invariant preferences, technology and laws of motions for exogenous variables. We relax this assumption and consider a class of infinite-horizon nonstationary models in which parameters can follow both deterministic and stochastic trends: the former trends take the form of anticipated shifts and drifts, and the latter trends take the form of Markov process with time-varying transition probabilities. We introduce a quantitative framework, called extended function path (EFP), for calibrating, solving, simulating and estimating such nonstationary models. We establish the existence and convergence (turnpike) theorems. We apply EFP to solve a collection of challenging nonstationary applications, including stochastic growth models with parameters shifts and drifts, capital augmenting technological progress, anticipated regime switches, time-trends in volatility of shocks and seasonal fluctuations. Also, we show an example of estimation and calibration of parameters in an unbalanced growth model using the data on the U.S. economy.
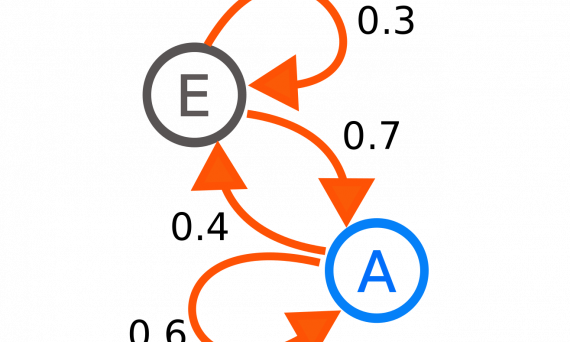
Image: Graph of a Markov chain, Joxemai4, wikipedia